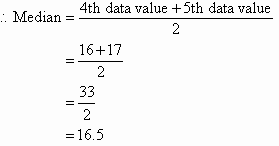Statistics Symbol
There are 24 letters of the Greek alphabet.
Home
Wednesday, July 28, 2010
Monday, July 26, 2010
Unit 1
Mean , Median , Mode
mean :The sum of a list of numbers, divided by the total number of numbers in the list. Also called arithmetic mean
15 13 18 16 14 17 12
Find the mean of this set of data values.
median :"Middle value" of a list. The smallest number such that at least half the numbers in the list are no greater than it. If the list has an odd number of entries, the median is the middle entry in the list after sorting the list into increasing order. If the list has an even number of entries, the median is equal to the sum of the two middle (after sorting) numbers divided by two. The median can be estimated from a histogram by finding the smallest number such that the area under the histogram to the left of that number is 50%
47 35 37 32 38 39 36 34 35
Find the median of this set of data values.
32 34 35 35 36 37 38 39 47
The fifth data value, 36, is the middle value in this arrangement.
Median =36
Find the median of the following data set:
12 18 16 21 10 13 17 19
Solution:
Arrange the data values in order from the lowest value to the highest value:
10 12 13 16 17 18 19 21
The number of values in the data set is 8, which is even. So, the median is the average of the two middle values.
The fourth and fifth scores, 16 and 17, are in the middle. That is, there is no one middle value.
mode :For lists, the mode is the most common (frequent) value. A list can have more than one mode. For histograms, a mode is a relative maximum ("bump"). A data set has no mode when all the numbers appear in the data with the same frequency. A data set has multiple modes when two or more values appear with the same frequency.
48 44 48 45 42 49 48
mean :The sum of a list of numbers, divided by the total number of numbers in the list. Also called arithmetic mean
Example 1
The marks of seven students in a mathematics test with a maximum possible mark of 20 are given below:15 13 18 16 14 17 12
Find the mean of this set of data values.
Solution:
So, the mean mark is 15.
Symbolically, we can set out the solution as follows:
median :"Middle value" of a list. The smallest number such that at least half the numbers in the list are no greater than it. If the list has an odd number of entries, the median is the middle entry in the list after sorting the list into increasing order. If the list has an even number of entries, the median is equal to the sum of the two middle (after sorting) numbers divided by two. The median can be estimated from a histogram by finding the smallest number such that the area under the histogram to the left of that number is 50%
Example 2
The marks of nine students in a geography test that had a maximum possible mark of 50 are given below:47 35 37 32 38 39 36 34 35
Find the median of this set of data values.
Solution:
Arrange the data values in order from the lowest value to the highest value:32 34 35 35 36 37 38 39 47
The fifth data value, 36, is the middle value in this arrangement.
Median =36
In general:
n is the number of data values in the sample
If the number of values in the data set is even, then the median is the average of the two middle values.
Example 3
Find the median of the following data set:12 18 16 21 10 13 17 19
Solution:
Arrange the data values in order from the lowest value to the highest value:
10 12 13 16 17 18 19 21
The number of values in the data set is 8, which is even. So, the median is the average of the two middle values.
Alternative way:
There are 8 values in the data set.The fourth and fifth scores, 16 and 17, are in the middle. That is, there is no one middle value.
Note:
- Half of the values in the data set lie below the median and half lie above the median.
- The median is the most commonly quoted figure used to measure property prices. The use of the median avoids the problem of the mean property price which is affected by a few expensive properties that are not representative of the general property market.
mode :For lists, the mode is the most common (frequent) value. A list can have more than one mode. For histograms, a mode is a relative maximum ("bump"). A data set has no mode when all the numbers appear in the data with the same frequency. A data set has multiple modes when two or more values appear with the same frequency.
Example 4
Find the mode of the following data set:48 44 48 45 42 49 48
Solution:
The mode is 48 since it occurs most often.
Note:
- It is possible for a set of data values to have more than one mode.
- If there are two data values that occur most frequently, we say that the set of data values is bimodal.
- If there is no data value or data values that occur most frequently, we say that the set of data values has no mode.
Subscribe to:
Comments (Atom)